Advent of Code 2023

Posted: Dec 4, 2023

My Goals

I don’t know how I could have missed that but I never encountered the Advent of Code event before this year, discovery done thanks to a colleague.

As XKCD coined it, I was one of the lucky 10 000.

I want to take the opportunity to do things “rights” ie:

Pytest
Cookiecutter (added later)
“Proper” things instead of the straighforward way. It means trying to document properly, to split into methods, to do things as pythonic as possible. Usage of non native libraries is valid.

I will document in this post the main interesting things for each day and all code will be present on the Github Repo

All Day X headers with 🔗📄 will be a link to the Github day code.

Day 1 🔗📄

The difficult part was the part 2 with the interpretation of sevenine is 79 whereas my initial interpreation was it to be 7ine. It led to a nice recursive function to parse the first interpretation but not needed at the end !

Second part was easy with a straighforward regex looking for overlap with this module:

restr = re.compile(r"(\d|one|two|three|four|five|six|seven|eight|nine)")
results = [word2nums[x] if not x.isdigit() else x for x in restr.findall(line, overlapped=True)]

Usage of cookiecutter (template here)

❯ cookiecutter template
  [1/1] day (DAY): 14

Day 2 🔗📄

Quite simple one.

To be fancy, usage of Enum :

class Color(str, Enum):
    RED = "red"
    BLUE = "blue"
    GREEN = "green"

Usage of reduce to compute the product of all elements in a sequence:

from functools import reduce
import operator
minballs = [1, 2, 3, 4, 5]
product = reduce(operator.mul, minballs)
print(product)  # This will print 120

Day 3 🔗📄

The base idea on my side for this one is to use networkx and to create a graph of positions (the grid coordinates), with the gears and partnumber as node linked to the positions.

Finding the answers is just a matter of finding the neighbours.

Usage of itertools for the neighbour generation:

    # Set up movement offsets for non-diagonal neighbors
    offsets = [-1, 0, 1]
    # Use itertools.product to generate all combinations of offsets
    directions = list(itertools.product(offsets, repeat=2))

Reuse of reduce(operator.mul,xxx)
Usage of lookahead for the parsing:

    # Parse the line (match number OR match all except numbers and dots)
    parse = re.compile(r"\d+|[^\d\.]")

Day 4 🔗📄

An easy part one but a more complicated rule to understand for part 2 (straightforward once you get it but still a “strange rule”).

Interesting points:

Using set intersection ( winnings = numberplayed & numberresults)

s1 = {0, 1, 2}
s2 = {1, 2, 3}
s_intersection = s1 & s2
print(s_intersection)
# {1, 2}

The old defaultdict as counter !
```
total = defaultdict(int)
```
Part 2 reminded me of the chess and wheat problem :

Day 5 🔗📄

Day 5 part 1 is “easy” and kind of want to go to part 2 with the same logic but :

The bruteforce method doesn’t work and doing seed by seed is not doable considering the size of the numbers. You need to redo it with ranges calculation but then you have to split you ranges when you have values mapping to themselves in one way and the others mapping on the able in another way. And rince and repeat with the others mapping tables.

From a code perspective, I used the itertools.chain.from_iterable to flatten the list of list of outgoing location (in my case twice as the structure was double nested):

list(itertools.chain.from_iterable([["a", "b", "c"], ["d", "e"], ["f"]]))
# ['a', 'b', 'c', 'd', 'e', 'f']

Day 6 🔗📄

Day 6 part 1 is quite trivial and part 2 was straightforward if you were reusing the previous code.

But seeing this on the web made me think that the solution could have been smarter. One blank paper later and the solution is quite simple in fact. Here it is :

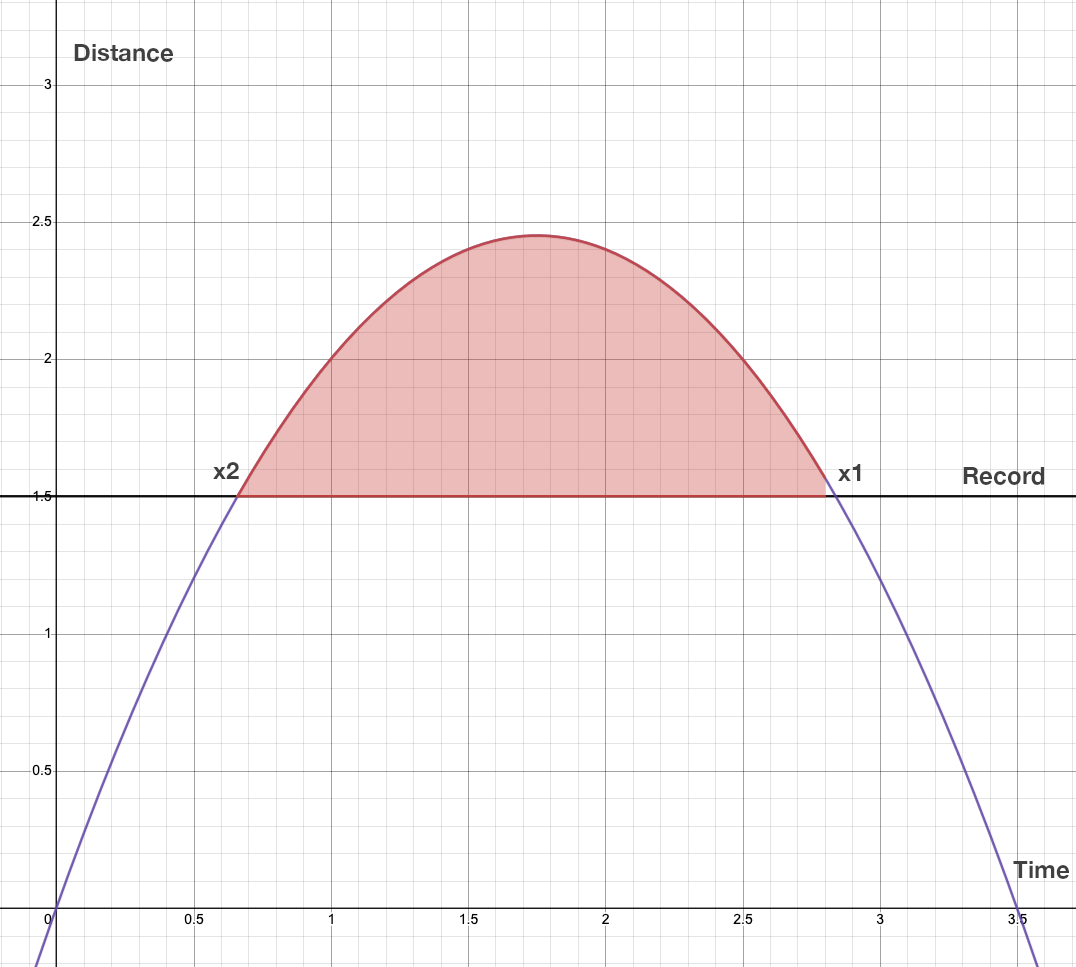
$$\text{We have seen in part1 that: \ } f(t)=(T-t)t\ \text{ where T is the total Time (Time in the input)}$$

$$\text{We want this function to be above the Record limit R (Distance in the input): \ } (T-t)t>R$$

$$\text{In fact we want the to know the intersection values where it became 0 (x1 and x2): \ } -t^2+Tt-R=0$$

$$\text{Considering }\ a^2x+bx+c+0, \text{we have : } a=-1,\ b=T,\ c=-R$$

$$\text{This is a quadatric equation solving with \ }x=\frac{-b\pm\sqrt[]{\Delta}}{2a}\ with\ \Delta=b^2-4ac$$

$$\text{We need the number of “ways” that can be expressed with: } S = x_1-x_2$$

$$S= \frac{-b+\sqrt[]{\Delta}}{2a} - \frac{-b-\sqrt[]{\Delta}}{2a}$$

$$2aS= -b+\sqrt[]{\Delta}+b+\sqrt[]{\Delta}$$

$$2aS= 2\ \sqrt[]{\Delta}$$

$$with\ a=-1\ S= \sqrt[]{\Delta}$$

$$\text{The solution is }\large S=\sqrt[]{T^2-4R}$$

One interesting point in term of code was the usage of dict(zip(times, distances)) to create a dict from two lists.

keys = ['a','b','c']
values = [1,2,3]
dict(zip(keys,values)) # {'a': 1, 'b': 2, 'c': 3}

Day 7 🔗📄

Day 7 was parsing a poker hand with specific rules. It was quite fun but “easy” as long as you kept close attention to the exact rules.

From a code point of view:

it was the occasion to re-implement class based methods, here is a short example (PokerHand is more lengthy):

class Card(object):
    figure = {
        "A": 14,
        "K": 13,
        "Q": 12,
        "J": 11,
        "T": 10,
    }

    def __init__(self, card):
        self.card = card

        if self.card.isdigit():
            self.power = int(self.card)
        else:
            self.power = self.figure[self.card]

    def __str__(self):
        # Used when string conversion
        return f"<{self.card}>"

    def __repr__(self):
        # Used when terminal representation (ie when printing a list of objects)
        return f"<{self.card} : {self.power}>"

    def __gt__(self, opposing):
        # greater than
        return self.power > opposing.power

    def __eq__(self, opposing):
        # equality
        return self.power == opposing.power

And sorted is always useful ! highest = sorted([Card(x) for x in remains], reverse=True)
Coming back from later days, I totally should have used a Dataclass for this one.

Day 8 🔗📄

Day 8 was figuring how to navigate a labyrinth with instructions. NetworkX to the rescue once again !

It took the occasion to redo an overview of the graph libaries:

Good and fast community detection algorithms in graph-tool
igraph seems to be faster but modifying the graph once it’s constructed is harder compared to networks
nx-cugraph, a NetworkX backend that provides GPU acceleration to NetworkX with zero code change

But I used and know networkx since so long and in the current test case, it was fitting.

And the core algorithm become quite simple:

while current_node != target_node:
    # Wrapped the index to repeat the directions
    wrapped_index = i % len(directions) - 1
    direction = directions[wrapped_index]
    # Find the outgoing edge with the specified attribute
    next_edge = [(u, v) for u, v, attr in graph.out_edges(current_node, data=True) if attr.get("name") == direction]
    cur, next = next_edge[0]
    logger.debug(f"{i} Following {direction} edge from {cur} to {next}")
    current_node = next
    i += 1

Part 2 was trickier and the bruteforce (once again) fails. The main idea to debug that is to start to consider the lenght of each individual ghosts path. As we need to “align” them, it means find the least common denominator between them so they can all reach the same “end step” at the same time. It is quite easy with a recent version of python and math.lcm(*list)

Day 9 🔗📄

Reading Day 9 definitely rings a bell from the past mathematics I did: “hey this is the method of finite differences !”.

(I was tempted to cheat and use a library implementing this but this is remove part of the fun).

Part 1 is just implementing the algorithm (doing shallow copy is a reflex when implementing this quite of thing)

The part 2 was the most easy I had seen as in my mind “extrapolate backwards” == list.reverse() and done in 2min.

In term of code, the interesting points are:

Doing a shallow copy with line = lnext[:] # shallow copy. It is generally enough but sometime a deepcopy with copy.deepcopy() may be needed as :
- Shallow copies duplicate as little as possible. A shallow copy of a collection is a copy of the collection structure, not the elements. With a shallow copy, two collections now share the individual elements.
- Deep copies duplicate everything. A deep copy of a collection is two collections with all of the elements in the original collection duplicated.
list.reverse() to reverse in place a list (did it twice in this day)

Btw, this article shows that the faster way to do it would be with a list comprehension but list.reverse() is just much more cleaner.

# Reverse a Python list with a List Comprehension
original_list = [1,2,3,4,5,6,7,8,9]
start = len(original_list) - 1
reversed_list = [original_list[i] for i in range(start, -1, -1)]
print(reversed_list)

all(list) / any(list) are definitely useful (in my case the condition to check the last line of 0 was while not all([x == 0 for x in line]) as doing the sum to 0 was messing up the tests when negative values entered the game)

Day 10 🔗📄

🛠 (Sunday is family day, will check later)

Day 11 🔗📄

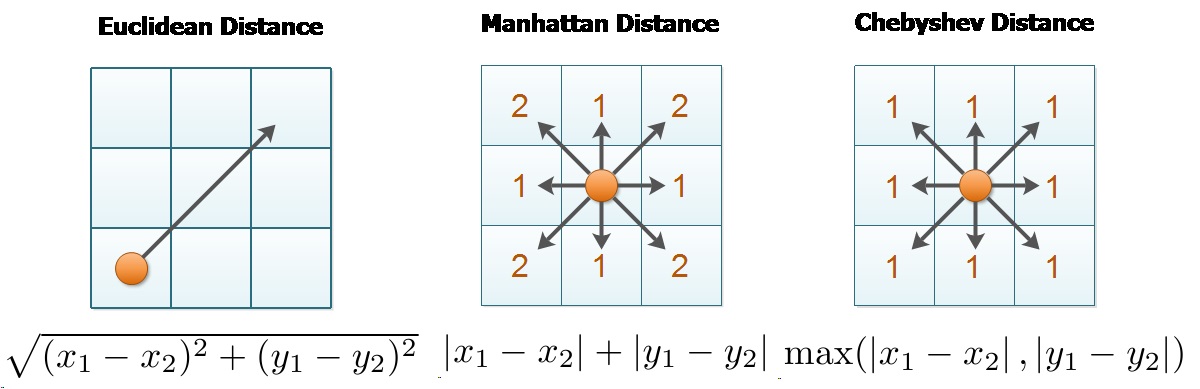
distances

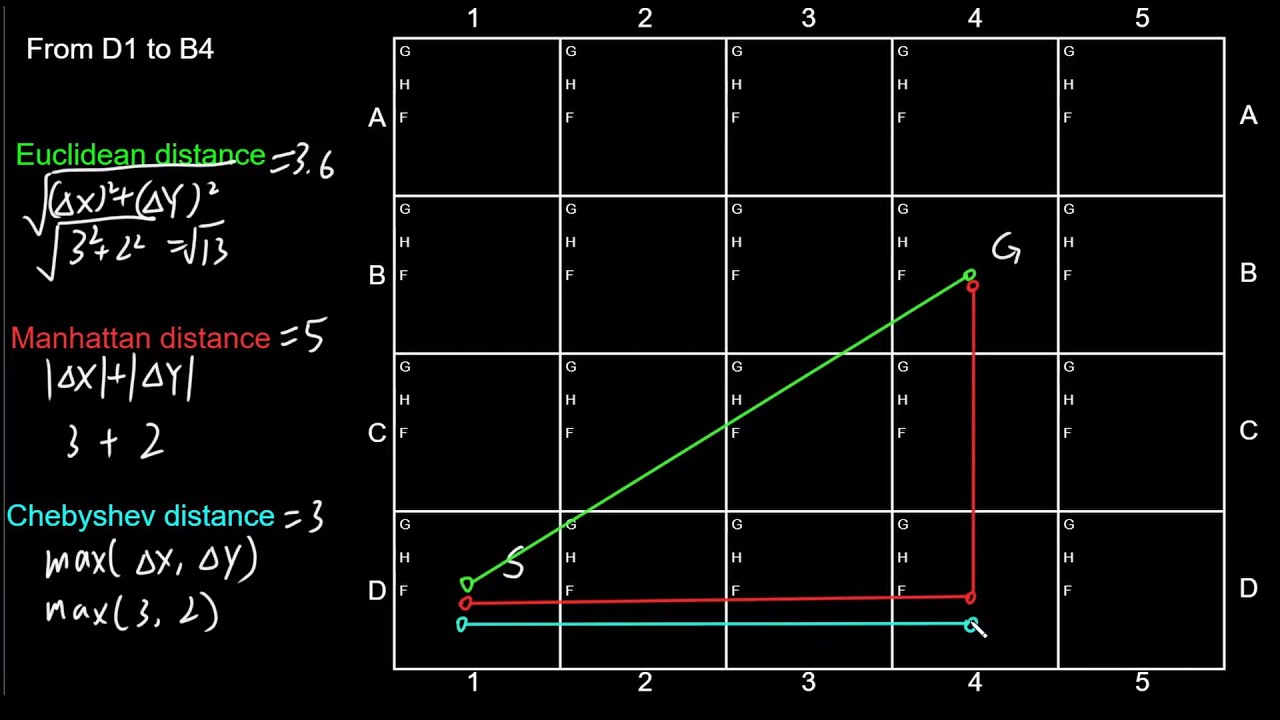
maxresdefault-171956676

The frustrating part of this one is initially implementing the Chebyshev distance because I badly read the rules instead of the Manhattan distance as it is when you read carefully. And spending time debugging in others parts of the code where the the issue was just the distance methodology…

Given two points $$\text P_1(x_1, y_1)\ and\ P_2(x_2, y_2)$$

Manhattan Distance:, the Manhattan distance between these points is calculated as:

$$\text{Manhattan Distance} = |x_2 - x_1| + |y_2 - y_1|$$

It represents the sum of the absolute differences of their Cartesian coordinates.

Chebyshev Distance: The Chebyshev distance between these points is given by:

$$\text{Chebyshev Distance} = \max(|x_2 - x_1|, |y_2 - y_1|)$$

It is the maximum of the absolute differences of their Cartesian coordinates.

In terms of code:

This one was also the occasion for me to play with numpy arrays as I’m more used to dataframes. (a lot of the logics applies)
Getting all unique pairs of coordinates is easy with itertools !

{ f"{pair[0]}-{pair[1]}" : manhattan_distance(pair[0], pair[1]) 
                          for pair in itertools.combinations(hash_coordinates, 2) }

I also adopted a new way of getting the file input with:

from pathlib import Path
data = Path(__file__).with_name(inputdata).read_text().splitlines()

Day 12 🔗📄

⚠️ [20231212] I will temporary stop until the week-end as I cannot cope with work, family as well as keeping up with Advent of code !

⚠️ [20231226] Starting this day, I will concentrate only on part 1 as Part 2 usually takes too long to do properly. In a second time (probably along the first semester of 2024, I will go back on the second parts not done quickly)

In terms of code:

Usage of dataclass. A dataclass mainly holds data and is flexible with no strict rules. You make it using the @dataclass decorator. This type of class automatically lets you create, show, and compare its instances easily. In the current case, I wanted to use it to store the records. However I wanted to have the “parsing” part inside the class. So I used the init=False on the args and the post_init function to do so:

from dataclasses import dataclass, field

@dataclass
class SpringRecord:
    raw_data: str
    record: str = field(init=False)
    damaged: tuple = field(init=False)

    def __post_init__(self):
        # Parse the string from the text record into the dataclass
        record = self.raw_data.split()[0]
        damaged = tuple(int(x) for x in self.raw_data.split()[1].split(","))
        self.record = record
        self.damaged = damaged

# Init is done with SpringRecord(raw_data)

Usage of itertools.product to generate the valid combinations positions. itertools.product is used to compute the Cartesian product of input iterables. It returns a generator that produces tuples of all combinations of elements from each iterable.

from itertools import product

digits = [0, 1]
letters = ['A', 'B']

# Generate all combinations of one digit and one letter
combinations = list(itertools.product(digits, letters))

print(combination_list)
# [(0, 'A'), (0, 'B'), (1, 'A'), (1, 'B')]

If you have a list of Boolean and you sum them, then True equal 1 and False equal 0. So sum(booleanlist)is equivalent to the number of True.

Day 13 🔗📄

In terms of code:

Usage of itertools.groupby. The operation of groupby() is similar to the uniq filter in Unix. It generates a break or new group every time the value of the key function changes (which is why it is usually necessary to have sorted the data using the same key function). In the code, it was used to split the text block separated with blank lines (more elegant than going over all the lines and stacking if not blank and moving to a new stack if blank):
```
  # Group lines by whether they're blank or not (like uniq in Unix)
  groups = groupby(lines, key=lambda x: x.strip() != "")
  # Extract groups of non-blank lines (cf key)
  return [list(group) for key, group in groups if key]
```
Usage of numpy vectorized operations instead of a loop to find the mirrored line (if n-1 == n line, we have our mirrored inflection part). As before, I wanted to force myself to use numpy vectorized instead of a simple loop.

In this code, pattern[:-1] represents all rows except the last, and pattern[1:] represents all rows except the first. The np.equal function compares these slices element-wise. The np.all function with axis=1 then checks if all elements in each row are equal, resulting in a boolean array where True indicates identical consecutive rows. Finally, np.where finds the indices of True values in this boolean array.
```
# Compare each row with its next row
identical_rows = np.all(np.equal(pattern[:-1], pattern[1:]), axis=1)
# Find the indices where rows are identical
identical_indices = np.where(identical_rows)[0]
```

Finding the mirror once you got the indices is just a matter of selecting on both side on the indices and flipping the second part to compare if both are equal (here example for column):

pivot = index.index + 1
to_border = min(pattern.shape[1] - pivot, pivot)
first_part = pattern[:, pivot - to_border : pivot]
second_part = pattern[:, pivot : pivot + to_border]
potential_mirrored_part = np.fliplr(second_part)
is_mirror = np.array_equal(first_part, potential_mirrored_part)

As a reminder here is a how to slice 2d array in Numpy:

To select rows from i to j: array[i:j, :]. To select columns from k to l: array[:, k:l]

rows_1_to_2 = array[1:3, :]  # Second and third row
cols_1_to_2 = array[:, 1:3]  # Second and third column

To select rows/columns with a certain step: array[start:stop:step, start:stop:step]

every_other_row = array[::2, :]  # Every other row
every_other_col = array[:, ::2]  # Every other column

Negative indices count from the end of the array. For example, -1 is the last item. A negative step reverses the direction of the slice.
```
reverse_rows = array[::-1, :]  # All rows in reverse order
reverse_cols = array[:, ::-1]  # All columns in reverse order
```

You can use arrays of integer indices to specify which rows or columns to select.

row_indices = np.array([0, 2])  # Array of row indices
selected_rows = array[row_indices, :]  # Selects first and third rows

This technique involves using an array of boolean values to select elements.

mask = np.array([True, False, True])
selected_rows = array[mask, :]  # Selects rows where mask is True

You can combine the above methods to create more complex slices.

subset = array[1:3, 0:2]  # A 2x2 subarray from the original array

Day 14 🔗📄

In terms of code:

Numpy to the rescue once again. It is an exercice to think in term of matrix/vector instead of always iterating over all rows/columns. For example, to count how many “balls” where present on a row (if you remember, I said earlier that True is counted as “1”):
```
# Create a boolean mask where rocks are True
ball_mask = original_array == ball_symbol
# Count rocks in each row
ball_counts = np.sum(ball_mask, axis=1)
```
To create a decremented array (10,9,8, …) instead of using a list enumeration with range(10, 0, -1), you can do in numpy the same with:
```
np.arange(start=len(countedballs), stop=0, step=-1)
```
I did a variation of the while loop by doing iterations of all cycles as I wanted to cache individual call.
```
total_cycles = itertools.islice(itertools.cycle(SPIN_CYCLE), number_cycle * len(SPIN_CYCLE))
```
``itertools.cycle(SPIN_CYCLE)creates an infinite iterator that repeats the elements inSPIN_CYCLE`.

itertools.islice(..., number_cycle * len(SPIN_CYCLE)) takes a slice of this infinite iterator, effectively limiting it to number_cycle repetitions of the SPIN_CYCLE.